The Project

Context

The project is based on a fly’s vision and behavior, through biomimicry. The general purpose is to create a bio-robot imitating the patterns and movements of a fly. Our specific approach focuses on the interaction between the photoreceptors of the fly’s eye and the perceived environment.

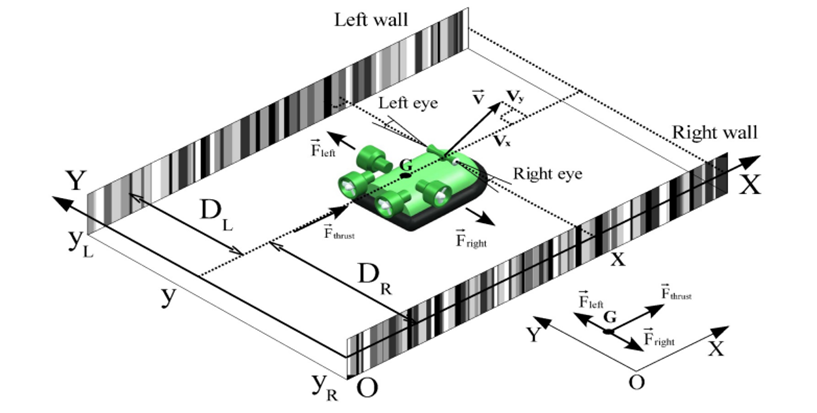
The point of the project is for the robot to move between two walls composed of stripes of different shades of gray. To achieve this project, we will assume that our fly only moves in a single direction and we want to simulate its vision considering the Gaussian sensitivity of the photodiodes.

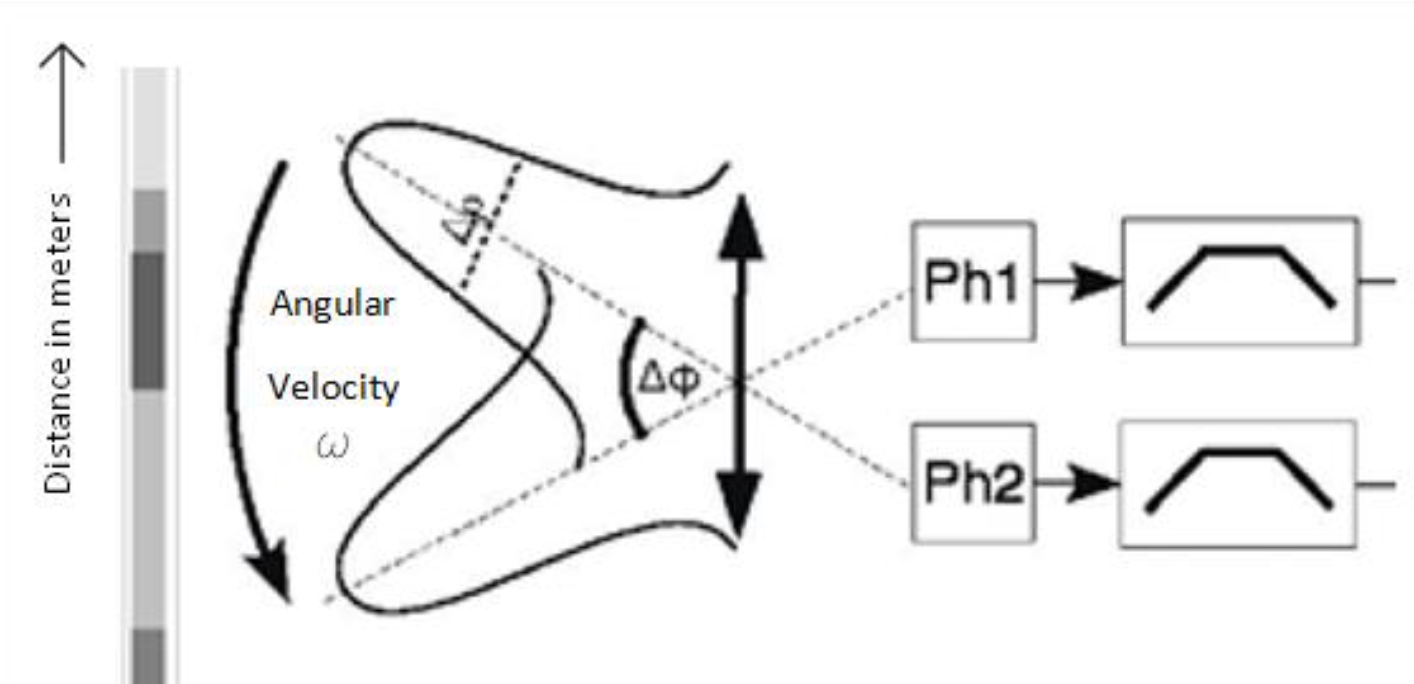
For simplicity’s sake, we are only going to consider two photoreceptors facing the same wall, and we are going to try to program the photoreceptors’ response.

Segmentation

Our project is composed of five major big steps:

Step 1: Create the environment function named env().

Step 2: Create a matrix to avoid recalculating the integrals of the Gauss curve

Step 3: Create the function giving the color observed by the fly according to time

Step 4: Analyze the fly's movement with the photoreceptors simulated in Simulink

Step 5: Put the output through a bandpass filter and finally convert it into 16 bits

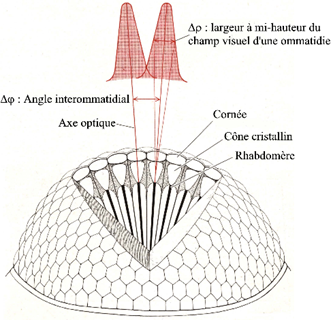
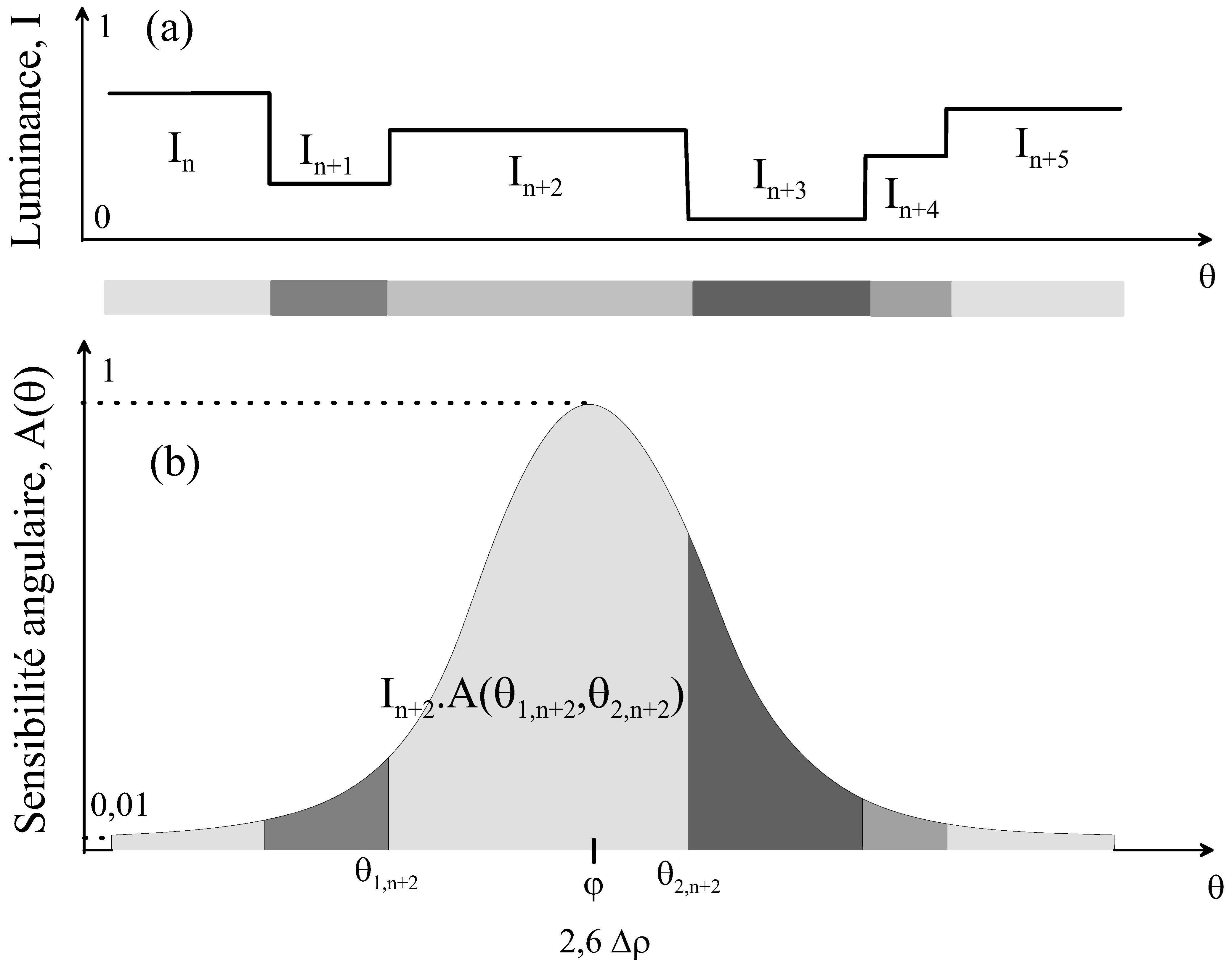
The photoreceptor has a Gaussian-shaped sensitivity, meaning that what is in the robot's peripheral vision won’t be as crucial in the calculation as what’s right in front of it.

The look-up table contains the integral of the Gaussian function, which represents the area of a certain shade of gray seen by the photoreceptor.

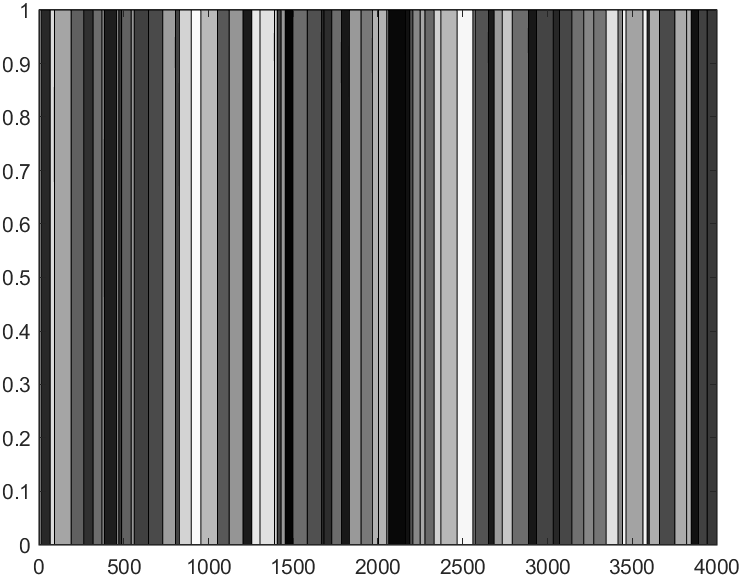
The environment is a four meters long gray-striped wall, with distinct shades. The distinction between the shades will be the benchmarks in our calculus.

Environment

The first step in our biomimicry project is to model the environment in which our fly will evolve. The model will only contain one dimension (the x-axis) for a 4-meter distance.

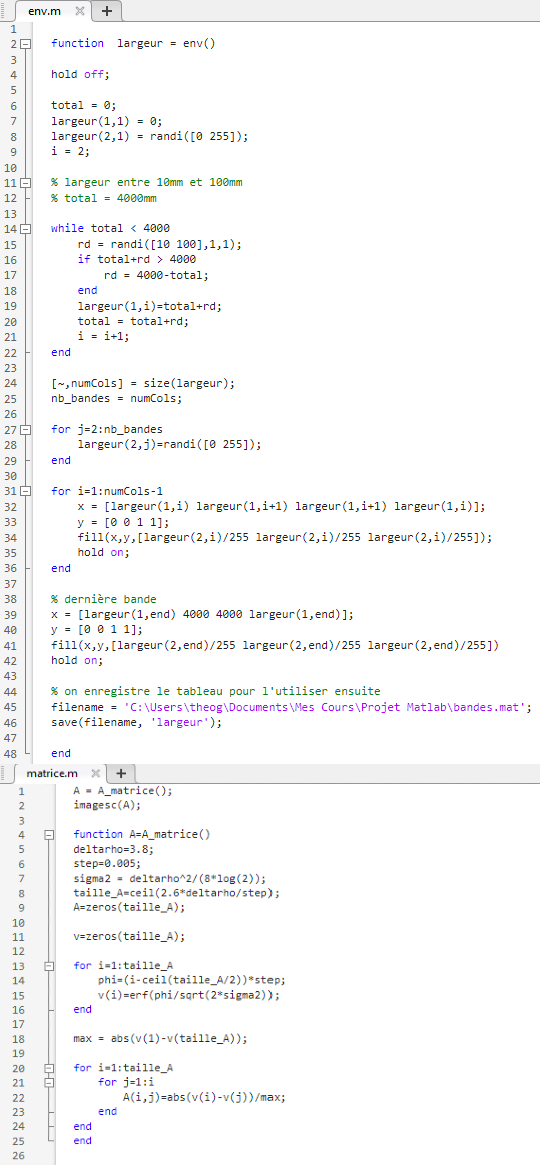
The key element in our model is that the environment is randomly generated by grey bands which length is included between 10mm and 100mm. The gray shade of every stripe is determined randomly, as well as the width thereof. Finally, the environment will have a resolution of Δx = 1mm.

Look-up tables

We just saw what the environment will look like, but our fly won't see it as clearly as we do. Indeed, it is the separation between two stripes that will determine the angle used later to calculate the sensitivity of the photoreceptor for the stripe considered. We will use a matrix to get what the photoreceptor perceives.

Thus, the next step consists of creating a matrix with all the predetermined areas needed later in the program, the A matrix. It will be a computational tool we will use to simplify the integral of the Gaussian curve of photoreceptors.

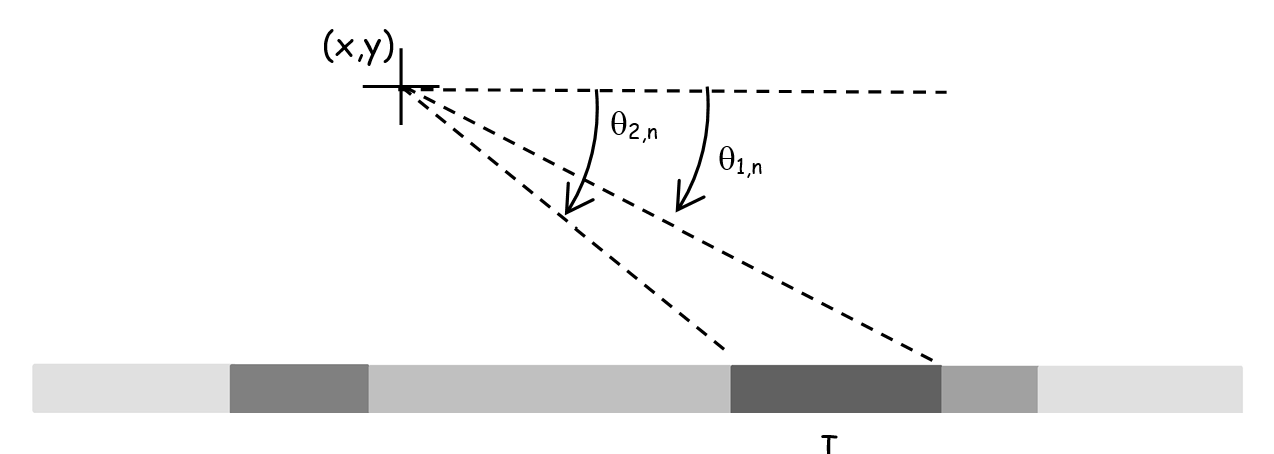
Basically, this matrix is used as a computational tool to simplify the integral of the Gaussian curve of photoreceptors as it represents a correspondence table thus allowing us to estimate the integral of the Gaussian sensitivity between two contrast transition angles. This matrix A will considerably reduce the execution time while modeling the photodiode outputs Ph1 and Ph2. Note that our matrix will be pre-calculated with a resolution δϕ = 0.005.

This function's parameters are the Δρ angle and the angular step (i.e., the resolution). At the end, the call A(angle1, angle2) returns the integral between two angular positions. Indeed, the photoreceptor output is calculated by piecewise integrating various luminances present in its visual field and weighting them by the Gaussian angular sensitivity.

The sensitivity of our photoreceptors depending on the angle is calculated with the Gaussian function, with φ as the azimuthal position and σ as the standard deviation.
where:

φ is the azimuthal position in the visual field of the photoreceptor

φ_max is the azimuthal position giving the maximum photoreceptor response

σ is the width at 95% of the height of the Gaussian (standard deviation)

Δρ is the width at 50% of the height of the Gaussian (angle of acceptance)

We also know that a relation exists between Δρ and σ:
At the end, the matrix contains every precalculated area of this Gaussian function, allowing us to determine exactly how much the photoreceptor is sensitive to a given stripe.

Simulating the photodetectors

We successfully created an environment for our experiment. Now, we have to deduce from it the way the fly's photoreceptors will perceive the size and color of every band. The process we used is complex and can be explained by the organigram below.

Visual field of the photodetectors

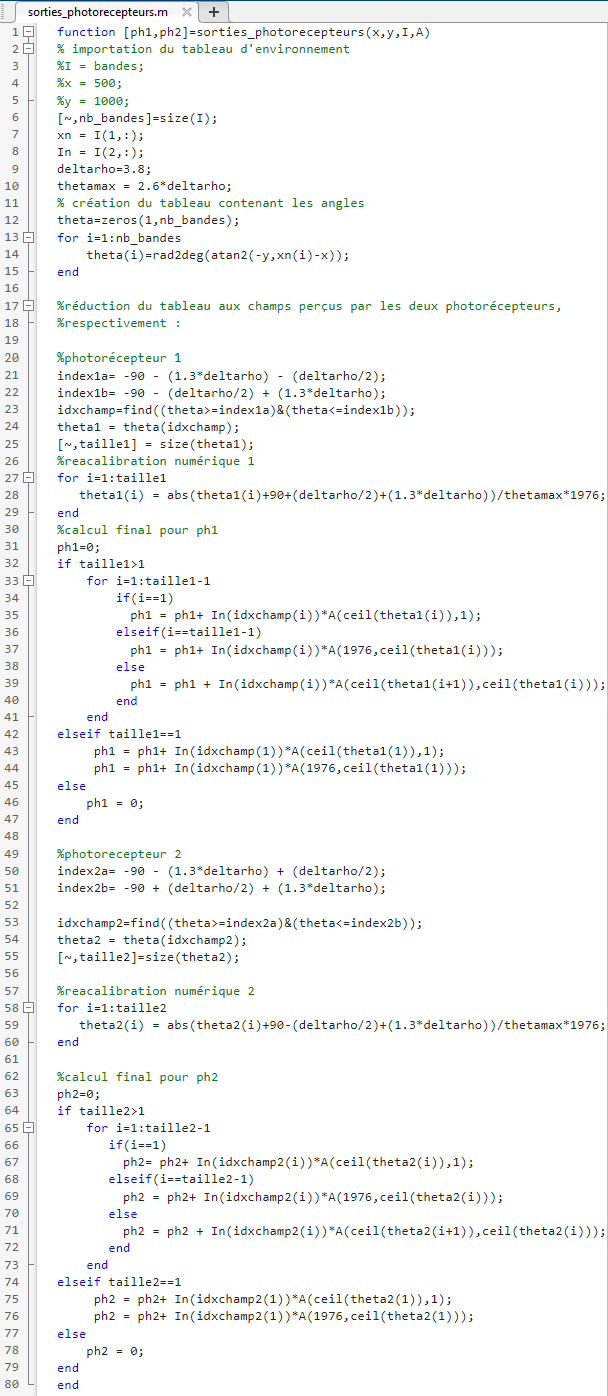
The MatLab function "find" allowed us to select the angles that are in the visual field of each of the photoreceptors, knowing that they are separated by ±Δϕ/2 from the wall.

For Ph1:
For Ph2:

Digital recalibration

During this step, we want to ensure that 1 ≤ θₙ ≤ 1976 in order to then exploit the matrix A.

The matrix A

The matrix A is used to determine the output of each of the photoreceptors by summation:
Please note that while calculating the global perception of the photoreceptor, we use a discrete sum instead of an integral to simplify the computer's calculating process.

Results and photodetector outputs

Simulation parameters

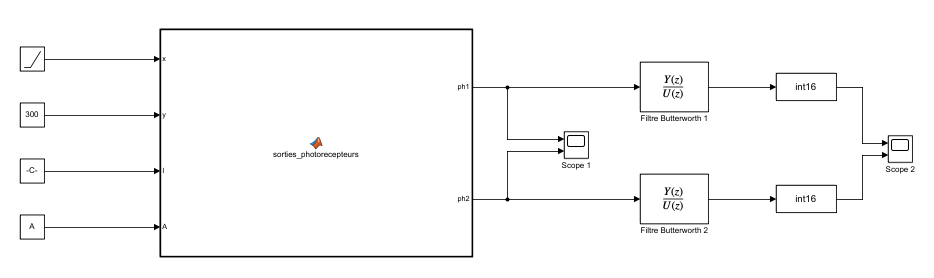
In order to correctly visualize the output of the two photodetectors, we used the Simulink software and we assumed that the fly moves parallel to the wall at 30 cm and a constant speed of 0.5 m/s, which is the role of the ramp block in our simulation.

Finally, we added a second-order digital bandpass filter [20 Hz; 116 Hz] and converted our data to 16 bits to simulate the analog-to-digital conversion of the microcontroller, with a temporal sampling frequency of 2 kHz.

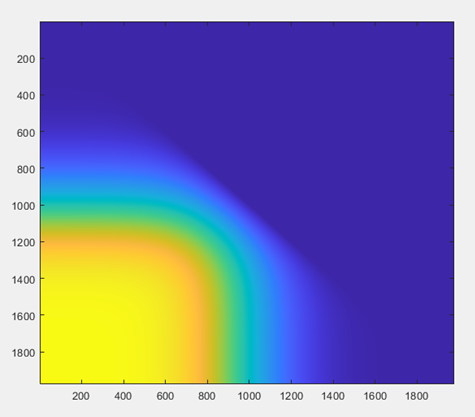
Output visualization

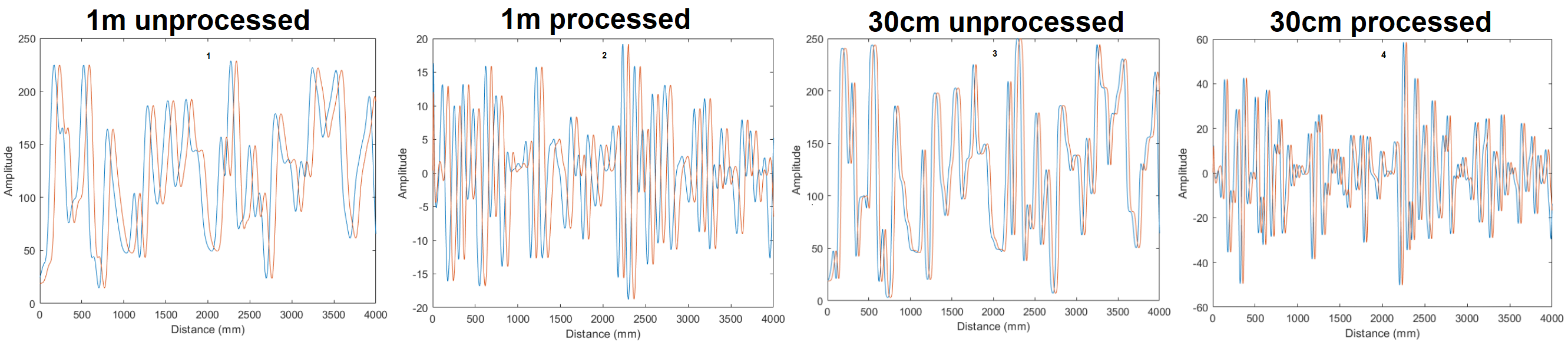
Interpretation

As we are moving from the wall, the two signals are shifting, which was expected. Moreover, it is clear that the results for the unprocessed output are smoother when we are farthest from the wall.

Conclusion

Our simulated environment is coherent and allows us to observe the evolution of the photoreceptor sensitivity. Our code is functional and could be implemented on a robot, proving the efficiency of biomimicry combined with new technologies.

Annexes